Faktorisieren eines quadratischen Terms
der Form T(x) = ax² + bx
+ c
mit Hilfe der binomischen Formeln
Umformen
einer Summe mit einem quadratischen Summanden ax² in ein Produkt aus Linearfaktoren
Die
binomischen Formeln liefern eine Methode, mit
deren Hilfe eine Summe in ein Produkt und ein Produkt in eine Summe umgeformt
werden kann. Da der Term T(x) = ax² + bx + c ein quadratischer Term ist, bieten
sich die binomischen Formeln dafür idealer weise gut an. Vergleicht man den
Term T(x) jedoch mit der 1. binomischen Formel so findet man mit Ausnahme des
Quadrats von x keine Ähnlichkeit mit dieser Formel a² + 2ab + b² = (a + b)²!
Wir müssen den Term also an die 1. binomische Formel anpassen. Das beginnt
schon bei der unterschiedlichen Verwendung von Buchstaben im Term und
in der binomischen Formel. Daher
ändern wir in der 1.
binomischen Formel den Buchstaben a in x um
und es wird aus a² + 2ab + b² = (a+b)² ▬▬► x² + 2xb + b² =(x +b)². Nun ist das b der
bin. Formel bei Leibe nicht das b im Term T(x).
Doch das stört erst einmal nicht. Vergleicht mit man nun die binomische
Formel mit dem Term kann eine gewisse Ähnlichkeit erkannt werden - wäre nicht a
als Faktor von x²! Dieser Faktor muss weg! Einfach weglassen verändert jedoch
den Term, was viele Schüler und leider auch Lehrer nicht daran hindert, es
trotzdem zu tun! Also braucht man eine mathematische Regel, die eine Umformung
des Terms in der gewünschten Weise erlaubt, ohne den Term zu verändern. Die
Methode heißt: ausklammern. Wir klammern den
Faktor a aus dem Term aus
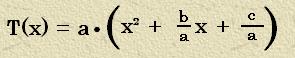
Leider wird die Ähnlichkeit eher dadurch verschlechtert!
Der Faktor a ist nun für die weitere Umformung von geringem Interesse. Deswegen
schreiben wir für T(x) = a● t(x) und bezeichnen mit t(x) den Faktor
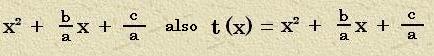
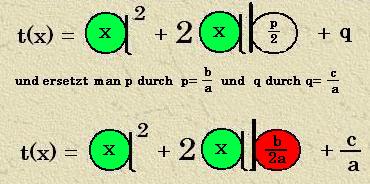
Das Umbenennen geht nun munter weiter. Auch ![]() bekommt einen neuen Namen üblicherweise p,
also p=
bekommt einen neuen Namen üblicherweise p,
also p=![]() , und ebenso nennen wir
, und ebenso nennen wir ![]() um
um
in ![]() = q. Der Term t(x)
= x² +
= q. Der Term t(x)
= x² + ![]() x +
x +![]() hat nun die Gestalt:
t(x) = x² + px + q. Selbst mit viel Phantasie kann man hier kaum noch eine
binomische Formel erkennen, von den Buchstaben mal ganz abgesehen. Aber Zahlen
sind Schall und Rauch und sie lassen sich so darstellen wie man gerade Lust
hat! Warum soll nicht 3 auch die Form III (römische Zahlzeichen) haben. Wichtig
ist nur zu wissen, was mit der Darstellung gemeint ist, so wie das Wort „Wort“
eine Ansammlung von Buchstaben bezeichnet. Also kann die Anpassung weiter
geführt werden! Im Term t(x) = x² + px+ q stimmt nun der erste Summand mit der binomischen
Formeln x² + 2xb + b² überein. Aber schon der zweite Summand denkt nicht daran.
Doch auch hier gibt es eine einfache Umformung: Wir erweitern den Summand px
mit 2 zu 2
hat nun die Gestalt:
t(x) = x² + px + q. Selbst mit viel Phantasie kann man hier kaum noch eine
binomische Formel erkennen, von den Buchstaben mal ganz abgesehen. Aber Zahlen
sind Schall und Rauch und sie lassen sich so darstellen wie man gerade Lust
hat! Warum soll nicht 3 auch die Form III (römische Zahlzeichen) haben. Wichtig
ist nur zu wissen, was mit der Darstellung gemeint ist, so wie das Wort „Wort“
eine Ansammlung von Buchstaben bezeichnet. Also kann die Anpassung weiter
geführt werden! Im Term t(x) = x² + px+ q stimmt nun der erste Summand mit der binomischen
Formeln x² + 2xb + b² überein. Aber schon der zweite Summand denkt nicht daran.
Doch auch hier gibt es eine einfache Umformung: Wir erweitern den Summand px
mit 2 zu 2![]() x , und schon sieht
t(x) = x² + 2
x , und schon sieht
t(x) = x² + 2![]() x + q der binomischen
Formel sehr viel ähnlicher:
x + q der binomischen
Formel sehr viel ähnlicher:
Nun fehlt nur noch der Summand b² der bin.
Formel. Aber auch hier stellt die Mathematik
ein ideales Hilfsmittel
zur Verfügung: Die Zahl Null! Die
Null ist eine Zahl mit bemerkenswerten Eigenschaften. Mit so bemerkenswerten
Eigenschaften, dass es eine Beleidigung für die NULL ist, einen Menschen als
Null zu bezeichnen. Eine dieser Eigenschaften besteht darin, dass sie immer da
ist (für welchen Menschen gilt das schon?), auch wenn man sie nicht vermutet
oder sieht! So ist 1=1+0 oder allgemein
dargestellt: a= a+0. Also sagen wir unseren Zauberspruch: Null erscheine im
Term t(x) und schon ist sie da:

Aber die Null hat noch eine weitere
Eigenschaft: Sie kann auch Zahlen hervorzaubern: 0 = 1 – 1 oder wieder
allgemein: 0 = a – a! Mit dieser
Eigenschaft können wir nun den Summand b² hervorzaubern:
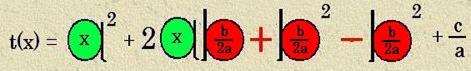
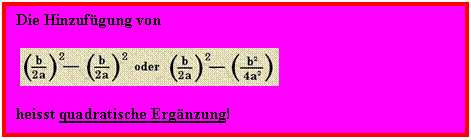
Nun sollte eigentlich jeder die 1. binomische Formel wiedererkennen!
Trotzdem noch einmal mit Klammern und farbiger Unterlegung:
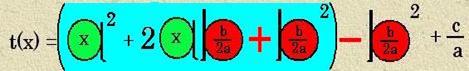
Diese
farbig unterlegten Summanden lassen sich mittels der 1.
binomischen Formel: a² + 2ab + b² = (a +
b)² zusammenfassen:

Ohne Hilfe
hat t(x) nun die Form t(x) = 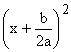 –
– 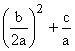
Wenn nun
die Klammer um 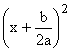 zu einem a ergänzt
wird, dann erhält man für t(x) die Darstellung
zu einem a ergänzt
wird, dann erhält man für t(x) die Darstellung

Ohne große
Phantasie erkennt man hier einen Teil der 3.
bin. Formel!
a² - b² = (a-b) (a+b)
Zu diesem Zweck müsste man in t(x) den Teil – 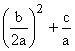 so umformen, dass dort
das Quadrat einer noch unbekannten Zahl steht, die in der Formel mit b
bezeichnet wird!
so umformen, dass dort
das Quadrat einer noch unbekannten Zahl steht, die in der Formel mit b
bezeichnet wird!
Die beiden Summanden – ![]() und
und ![]() müssen deshalb zuerst
zu einem Summanden zusammengefasst werden, der ein negatives Vorzeichen haben
muss. Deswegen klammern wir -1 aus
beiden Summanden aus:
müssen deshalb zuerst
zu einem Summanden zusammengefasst werden, der ein negatives Vorzeichen haben
muss. Deswegen klammern wir -1 aus
beiden Summanden aus:
– 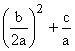 = (– 1)
= (– 1) 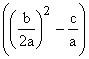
Nun
quadrieren wir den Bruch ![]() =
= ![]() unter Verwendung der Potenzgesetze:
unter Verwendung der Potenzgesetze:
= (– 1) 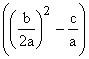 = (– 1)
= (– 1) 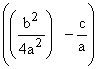
und addieren (subtrahieren) die
beiden Brüche in der Klammer nach den Regeln der Bruchrechnung : Hauptnenner
bilden und Zähler addieren (subtrahieren)
= (– 1) 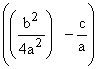 = (– 1)
= (– 1) 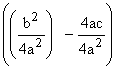 = (– 1)
= (– 1) 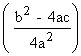
Nach dieser
Umformung sieht der Term t(x) so aus

Fast schon wie die 3. binomische Formel! Wenn doch nur statt b das
Quadrat von b stünde! Auch hier bietet die Mathematik eine elegante Lösung an!
Es ist bekanntlich a = ![]() für a>0! Genau diese Regel hilft uns nun weiter und es
wird
für a>0! Genau diese Regel hilft uns nun weiter und es
wird

Damit ist
nun die Struktur der 3. binomischen Formel erreicht und sie kann angewendet
werden:

Ohne die
symbolischen a und b hat t(x) die Form

Damit ist
das Ziel erreicht, den Term T(x) = ax² +bx +c in ein Produkt aus Linearfaktor
zu zerlegen:
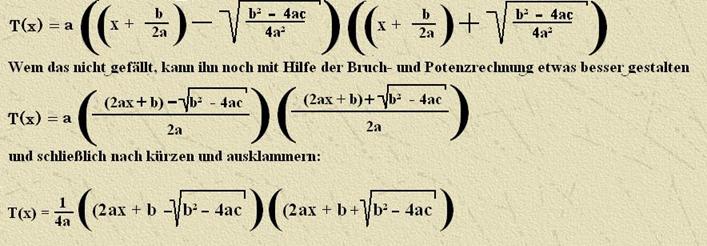
eine gar
nicht mal so komplizierte Form!
Hier noch
einmal die Zusammenfassung aller Schritte

Setzt man
für ![]() = p und für
= p und für
![]() =q wie es oben schon getan wurde, dann hat der Term
=q wie es oben schon getan wurde, dann hat der Term
T(x) =
a(x² +
![]() x +
x + ![]() ) die Form
) die Form

Sucht man
nun nach einer Zahl x, so dass T(x) = 0 wird, so geht der Term T(x) = ax² + bx + c in
die quadratische
Gleichung 0 = ax² + bx + c über und man erhält aus
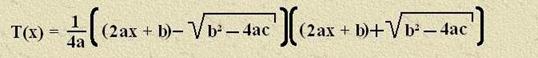
die Lösung
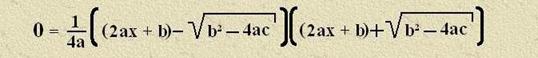
Mit dem
bekannten Satz: Hat ein Produkt den Wert 0, so ist mindestens einer seiner
Faktoren Null, erhält man die Gleichungen:
1. (2ax + b) – ![]() = 0
= 0
2. (2ax + b) + ![]() = 0
= 0
und daraus
die Lösungen
1.
x1
= ![]()
2.
x2
= ![]() (Diese Darstellung
heißt a-b-c-Formel oder auch Mitternachtsformel)
(Diese Darstellung
heißt a-b-c-Formel oder auch Mitternachtsformel)
Man sieht auch
sofort, dass der Radikand b² - 4ac der Wurzel die Lösungen bestimmt. Man nennt
b²- 4ac auch Diskriminante.
Ist b² - 4ac>0 dann hat die Gleichung ax² + bx + c=0 zwei
unterschiedliche Lösungen.

Ist b² - 4ac=
0 dann hat die Gleichung ax² + bx + c = 0 genau eine Lösung, weil in diesem
Falle die Diskriminante den Wert Null hat und ![]() .
Die Lösungen sind x1 = x2 =
.
Die Lösungen sind x1 = x2 = ![]() .
.
Ist b² -
4ac< 0 dann hat die Gleichung ax² + bx + c = 0 keine reelle Lösung, weil es
keine reelle Zahl gibt, deren Quadrat negativ ist.
Die
Lösungen x1 und x2 sind nur mit Hilfe der komplexen
Zahlen darstellbar.
Die
quadratische Gleichung 0 = ax² + bx + c kann auch auf beiden Seiten mit a geteilt werden:
0 = ax² + bx + c │:a
Man beachte:
0:a = 0 und auf der rechten Seite ist
eine Summe zu teilen, d.h
jeder Summand muss mit a geteilt
werden
0 = x² + ![]() x +
x + ![]() setzt man für
setzt man für ![]() = p und für
= p und für ![]() =q so erhält die quadratische Gleichung die Form
=q so erhält die quadratische Gleichung die Form
0 = x² + px + q
│ quadratische Ergänzung
einfügen 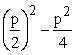
0 = x² + px + 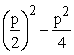 +q │
+q │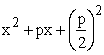 mit der bin. Formel zusammenfassen zu
mit der bin. Formel zusammenfassen zu 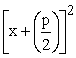
0 = 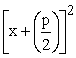 —
— ![]() +q │—
+q │—
![]() +q fasst man zusammen zu
+q fasst man zusammen zu 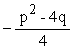
0 = 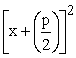 —
— 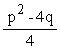 │aus
│aus 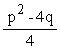 wird
wird 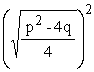
0 = 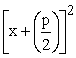 —
—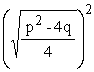 │ nun
wird mit Hilfe der 3. bin Formel
│ nun
wird mit Hilfe der 3. bin Formel
0 = 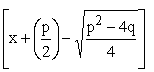
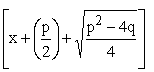
Und wieder mit dem bekannten Satz: Hat ein Produkt den Wert 0, so ist mindestens
einer seiner Faktoren Null, erhält man die Gleichungen:
1.
0= 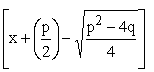
2.
0=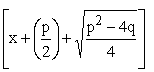
und aufgelöst nach x
x1 = 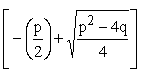 und
und
x2 = 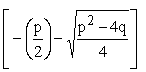 oder nach
teilweisem Wurzelziehen
oder nach
teilweisem Wurzelziehen
x1 = ![]() und
und
x2 = ![]() allgemein
bekannt unter dem Namen p-q-Formel.
allgemein
bekannt unter dem Namen p-q-Formel.

Wozu nun
dieser ganzen Aufwand? Wer mit Ausnahme von armen geplagten Schülern und
betroffenen Eltern braucht so etwas?
Zunächst
ist eine sehr schöne Anwendung der vielgehassten binomischen Formeln und
anderer mathematischer Gesetze. Doch was nützt mathematische Schönheit oder
mathematische Kunst, wenn sie (wie Kunst oder Musik) nur zum Staunen da ist?
In der Schulmathematik ist diese Umformung so unverzichtbar wie der
Satz des Pythagoras oder die triviale Einsicht, dass jedes Produkt, in dem ein
Faktor den Wert Null hat, selbst den Wert Null hat.
Eine
Anwendung habe ich Ihnen oben genannt: Das Lösen einer quadratischen Gleichung:
ax² + bx + c = 0 und für Zahlenfetischisten ein Zahlenbeispiel: 0,5x² - 6x = 9.
Lieber Leser dieser Seite, sofern Sie nicht Lehrer, Schüler oder
Mathematikdozent sind, sondern mit beiden Beinen im realen Leben stehen, nennen
Sie Beispiele aus Ihrem beruflichen Alltag, bei denen das hier beschriebene
Problem Anwendung findet. Eines kann ich selbst liefern:

Helfen Sie also bitte mit, Beispiele zu geben, in denen das Lösen einer
quadratischen Gleichung im beruflichen – nicht schulischen Alltag – wenigstens
einmal im Leben vorkommt. Lehrer- und Elterngenerationen werden Ihnen diesen
Motivationsschub danken!
Übungsaufgabe mit Lösung 3x² + 6x - 2 = 0 │* 1/3 x² + 2x –
2/3 = 0 │ qE 1²- 1 x² + 2x +1² - 1
- 2/3= 0 │ 1. bin Formel x²+2x+1² = (x+1)² (x+1)² -
1-2/3 = 0 │ - 1 -2/3 = -5/3 = - (x+1)² - (x+1 - x+1 - (x+1 + __________________________________________________________________ Oder a=3 b=6 und c=-2
und mit Lösungsformel: 1.
x = 2. x = oder auch 3x² + 6x - 2 = 0 │* 1/3 x² + 2x –
2/3 = 0 │ p,q Formel p= 2 und q = -2/3 x1 = x1 = -1 + x1 = -1 + Alle Wege haben ihre Vor- und Nachteile. Man gewinnt
nichts, wenn man nur einen Weg als richtig zulässt. Ich persönlich ziehe
die erste Variante vor, weil dieser Weg den Schüler immer wieder zwingt, an
die binomischen Formeln zu denken und sie richtig anzuwenden. Viel
wichtiger noch ist, dass selten eine Lösung vergessen wird! Der Rechenaufwand
ist bei allen Wegen gleich! Bei komplizierten Ausdrücken oder wenn gar in
der Lösung noch eine Variable enthalten ist, dann ist der erste Weg
einsichtiger und zwingender! Ansonsten halte
es jeder wie er will, und wie er am besten und ohne Fehler klar kommt! Das Ende jeder
Kreativität ist der Schematismus!
![]()
![]() = 0 │3. bin.
Formel
= 0 │3. bin.
Formel ![]() ) (x+1 +
) (x+1 +![]() )=0
)=0 ![]() =0 ▬► x1= -1 +
=0 ▬► x1= -1 +![]()
![]() )=0 ▬► x2= -1 -
)=0 ▬► x2= -1 -![]()
![]() ▬► x1=
▬► x1=![]() → x1=
→ x1=![]() → x1=
→ x1=![]()
![]() ▬►
x2=
▬►
x2=![]() → x2=
→ x2=![]() → x1=
→ x1=![]()
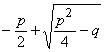 oder x2
=
oder x2
= 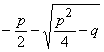
![]() oder x2
= -1 -
oder x2
= -1 -![]()
![]() oder x2= -1 -
oder x2= -1 -![]()